In many of my previous posts I have used the term column volume, typically abbreviated as CV, as a value used to help determine separation quality and loading capacity. However, I recently was asked a question about this topic from a chemist who understands the column volume concept but wanted to better understand its definition and how it is determined.
In this post I will explain what a column volume is and how it is determined empirically.
Some chemists think the internal volume of the or column – without packing material inside is the column volume. While useful in determining scale-up factors, the empty column’s volume is not the CV. The CV of any column is the volume inside of a packed column not occupied by the media. This volume includes both the interstitial volume (volume outside of the particles) and the media’s own internal porosity (pore volume). Combined, the two volumes constitute 70% to 80% of the packed column’s volume. Of course this means that the media only occupies 20% to 30% of the space in the cartridge.
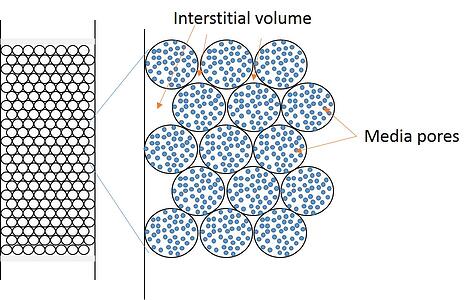 Figure 1. A graphical illustration depicting a packed flash cartridge bed with both media pores (blue) and interstitial volume between particles highlighted. The volume inside the particles and outside the particles create the column volume.
Figure 1. A graphical illustration depicting a packed flash cartridge bed with both media pores (blue) and interstitial volume between particles highlighted. The volume inside the particles and outside the particles create the column volume.
Media manufacturers always test their product to ensure it conforms to their specifications which is always expressed as a range. One of the primary tests performed on silica is a nitrogen BET analysis that measures both surface area and porosity. Here at Biotage, we test every batch of media we purchase to ensure it meets our specifications. The test results for any media batch are an average surface area and an average pore volume. From the surface area and pore volume the average pore diameter is calculated.
Most flash silica used in normal-phase chromatography has an average surface area of 500 m2/g and a calculated pore diameter of 60Å. This equates to a pore volume of 0.75 mL. How did I arrive at this value? I adjusted the equation below, which calculates pore diameter, to calculate pore volume.
PD = (40,000 * PV)/SA
Where:
- -PD = pore diameter in Angstroms (Å)
- -PV = pore volume in mL/g
- -SA = surface area in m2/g
- -40,000 = a unit conversion constant
-To back-calculate PV…
PV = (SA * PD)/40,000
Substituting values for surface area and pore diameter noted above, the equation becomes…
PV = (500 m2/g * 60Å)/40,000
Or
PV = 0.75 mL/g
So, if we multiply the pore volume (0.75 mL/g) by the amount of media in a column we obtain the approximate volume inside the particles in that cartridge. For example, if a flash column contains ten grams of silica and we multiply by 0.75 mL/g we obtain an intra-particle volume of 7.5 mL; this is not the column volume as it does not include the interstitial volume.
The interstitial volume factor, at least in slurry-packed HPLC columns, is approximately 0.4[1]. In dry-packed, larger particle flash columns I estimate the interstitial factor is about 0.45 because the particles are slightly less densely packed than the typical 3 to 10 micron HPLC column media.
Using the flash cartridge interstitial volume factor (0.45), the media amount in the cartridge (10 g), and that media’s pore volume (0.75 mL/g) we can estimate the 10 g packed cartridge’s column volume using the following equation:
CV = (Media weight (g)*media pore volume (mL/g))/(1 - interstitial volume factor)
Or
CV = (10 g * 0.75 mL/g)/0.55
Or
CV = 13.6 mL
Increasing the media’s porosity of course will increase the CV for any column packed with that larger porosity material.
Knowing the column volume helps determine purification run length, gradient profile, and solvent consumption, an important factor if a purification method requires scaling up.
If you want to learn more about flash chromatography, be sure to check out the white paper below on Inspiring Productivity in Modern Flash Chromatography!
[1] Neue, Uwe. HPLC Columns Theory, Technology, and Practice. Wiley-VCH 1997, p. 53

 Organic Workflow
Organic Workflow Peptide Workflow
Peptide Workflow Scale-Up Flash Purification
Scale-Up Flash Purification  Sample Preparation
Sample Preparation Biomolecule Purification
Biomolecule Purification Oligo synthesis
Oligo synthesis Scavengers and Reagents
Scavengers and Reagents Service & Support
Service & Support Accessories & Spare parts
Accessories & Spare parts Investors
Investors Reports & News
Reports & News The Share
The Share Corporate Governance
Corporate Governance Calendar
Calendar Sustainability
Sustainability Our Offering
Our Offering Our History
Our History Our Locations
Our Locations Leadership
Leadership